해당 글은 제가 모르는 부분을 디버깅하며 찾아가는 과정이기에 설명에 부족한 부분이 있을 수 있습니다
문제
방향그래프가 주어지면 주어진 시작점에서 다른 모든 정점으로의 최단 경로를 구하는 프로그램을 작성하시오.
단, 모든 간선의 가중치는 10이하의 자연수이다.
입력
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다.
둘째 줄에는 시작 정정의 번호 K가 주어진다. 셋째 줄부터 E개의 줄에 걸쳐 각 간선을 나타내는 세 개의 정수(u,v,w)가 주어진다. 이는 u에서 v로 가는 가중치 w인 간선이 존재한다는 뜻이다. u와 v는 서로 다르며 w는 10이하의 자연수이다.
서로 다른 두 정점 사이에 여러 개의 간선이 존재할 수도 있음에 유의한다.
테스트해 볼 입력데이터
5 6
1
5 1 1
1 2 2
1 3 3
2 3 4
2 4 5
3 4 6
dist[] -> 최단 경로
visit[] -> 배열을 방문했는지
graph -> 인접리스트를 구현함 가중치가 포함되어 있으므로 기본 int가 아닌 Node(정점, 가중치) 를 사용한다.
package com.example.algorithgm.dist;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Dist {
// 노드 확인 테이블
static ArrayList<ArrayList<Node>> graph = new ArrayList<>();
// 방문한 적이 있는지 체크
static boolean[] visit;
//최단 거리 값 확인
static int[] dist;
static class Node{
int v; //간선
int cost; //가중치
public Node(int v, int cost){
this.v = v;
this.cost =cost;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int v = Integer.parseInt(st.nextToken());//정점의 개수
int e = Integer.parseInt(st.nextToken());//간선개수
int k = Integer.parseInt(br.readLine());//시작정점
dist = new int[v+1];
visit = new boolean[v+1];
for(int i = 1; i <= v; i++){
dist[i] = Integer.MAX_VALUE; //최대값으로 모두 초기화한다/ 최단거리를 찾기위함
}
for(int i=0;i<v+1;i++){
graph.add(new ArrayList<>());
}
for(int i=0;i<e;i++){ //간선만큼 간선이 계속 주어지기 떄문에
// u -> v로 가는 가중치 w가 주어지낟.
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
graph.get(a).add(new Node(b, c));
}
//다익스트라 알고리즘 수행
dijkstra(k);
for (int i = 1; i <= v; i++) {
System.out.println(dist[i] == Integer.MAX_VALUE ? "INF" : dist[i]);
}
}
static void dijkstra(int start){
PriorityQueue<Node> q = new PriorityQueue<>((o1, o2) -> o1.cost - o2.cost);
q.add(new Node(start,0)); //자기 자신이므로 0
dist[start] = 0; //자신이므로 0처리
while(!q.isEmpty()){
//현재 최단 거리가 가장 짧은 노드를 꺼내서 방문처리
Node now = q.poll();
if(visit[now.v]){ //방문을 이미 했다면
continue;
}else{ //방문을 하지 않았다면
visit[now.v] = true;
for(Node next : graph.get(now.v)){
if(dist[next.v] > dist[now.v] + next.cost){
dist[next.v] = dist[now.v] + next.cost;
q.add(new Node(next.v,dist[next.v]));
}
}
}
}
}
}
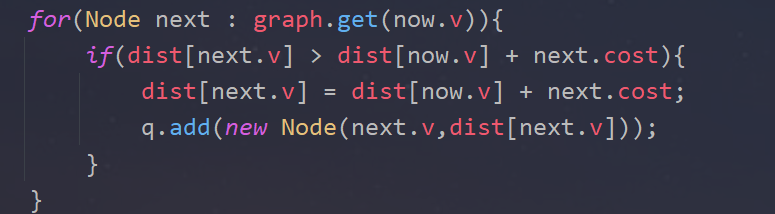
이 부분이 가장 이해가 가지 않았다. 하지만 이 부분은 디버깅으로 테스트 해봤다.
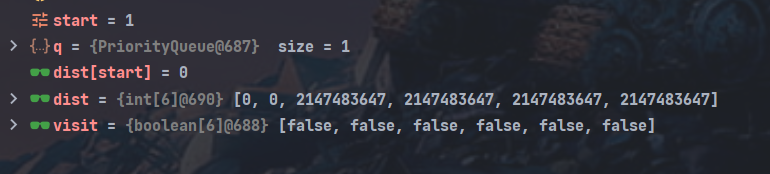
백준 문제에서 처음 들어온 값을 보면 start를 1로 주어지고 그 값부터 최단경로를 찾아 나서는데 dist[]은 1이 주어졌으므로 dist[1] = 0 (시작지점은 항상 0이 되어야함)이고 그 뒤에 값들은 Integer.MAX_VALUE이다(처음으로 경로를 찾게 되면 그 값으로 수정학 위해서이다)
while이 처음 들어올때

now 변수가 가르키는 정점들을 모두 조회한다. graph.get(now.v)


다시 위에 식을 살펴보면 바로 쉽게 알 수 있다. 입력 값 중에 한 줄을 보면 1 2 2 이다. 이건 1번 정점이 2번정점을 방향이 되어있고 해당 간선에 가중치는 2라는 것이다.
위에 디버깅 결과를 보면 next,cost는 다음 간선에 연결된 간선인데 간선 값이 2가 나온다. 주어진 값이 2이기 때문이다. next.v도 2이다. 결국 위에 if문은 if(dist[2] > dist[1] + 2) 계산이다.
즉, 현재까지의 최단 경로(지금까지 오는데 만난 가중치를 모두 더한 값)에서 다음 정점으로 가는데 만나는 가중치를 더한 값이 다음 간선에 최단경로보다 작냐고 묻는 것인데 여기서 dist는 위에 디버깅결과에서 볼 수 있듯이 모두 초기화 되어있다. 즉 말은 처음 한 번은 값 무조건 if문을 통과한다. ( 1번에서 2번을 처음간다는 가정하임) 그러면서 dist[2]는 값이 변경되고 해당 정점 2를 Queue에 넣는다. 하지만 여기서 for문은 1번이 가르키는 모든 정점을 다 보기에 BFS 성질인 것을 볼 수 있다. 그렇게 while문이 처음 돌때 해당 for문으로 1번이 가르키고 있는 정점들에 dist(가중치를 모두 더한 값)을 알 수 있다. 그렇게 알게 된 dist는 다음 정점을 타고갈 때 이용되게 된다.
다익스트라(Dijkstra) 최단 거리 알고리즘
방식은 너비 우선 탐색(BFS) 방식과 유사하다. 그러나 BFS는 가중치 각각 다른 간선에 대해서 최단거리를 찾을 수 없다
알고리즘 특징
- 가중치 그래프의 한 지점에서 그 외 다른 모든 지점까지의 최단거리를 구할 수 있다.
- 그래프 연결 관계(간선)를 리스트에 저장하는 인접 리스트를 사용한다.
- 가중치 그래프에서 음의 가중치를 가지는 간선이 존재하면 안된다.
초기화
다익스트라 알고리즘을 구현하는데 두 개의 배열이 필요하다.
- dist 배열 -> 각 정점들까지의 최단거리를 저장하는 배열이다. 시작 정점을 0, 그 외의 정점들을 무한대(제일 큰 값)으로
초기회해준다.
- visit 배열 -> 각 정점들의 방문여부를 체크하는 배열이다. 시작 정점은 방분 그 외의 정점들은 무방문 상태로 초기화한다.
종료조건
- 모든 정점이 방문되었다면 모든 정점에 대해서 최단거리를 구한 것이므로 알고리즘을 종료한다.
'알고리즘' 카테고리의 다른 글
| 백준 No.1931 회의실 배정 - JAVA (0) | 2023.02.02 |
|---|---|
| 백준 No.13305 주유소 - JAVA (0) | 2023.02.01 |
| 백준 No.1463 1로 만들기 - JAVA (0) | 2023.01.30 |
| 백준 No.2252 줄 세우기 - JAVA (0) | 2023.01.28 |
| Graph - BFS 간단 개념 및 코드(JAVA) (0) | 2022.12.22 |