문제
어떤 나라에는 1번부터 N번까지의 도시와 M개의 단방향 도로가 존재한다. 모든 도로의 거리는 1이다.
이 때 특정한 도시 X로부터 출발하여 도달할 수 있는 모든 도시 중에서, 최단 거리가 정확히 K인 모든 도시들의 번호를 출력하는 프로그램을 작성하시오. 또한 출발 도시 X로 가는 최단 거리는 항상 0이라고 가정한다.
예를 들어 K=4,K=2,K=1 일 떄 다음과 같이 그래프가 구성되어 있다고 가정하자
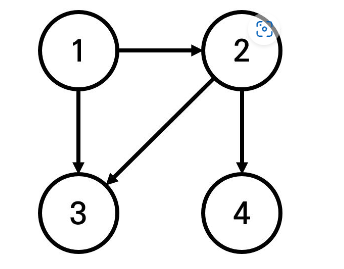
이 떄 1번 도시에서 출발하여 도달할 수 있는 도시 중에서 최단 거리가 2인 도시는 4번 도시 뿐이다. 2번과 3번 도시의 경우, 최단 거리가 1이기 때문에 출력하지 않는다.
풀이
- 방향성 그래프, 거리를 구한다 --> 다익스트라
- 출발점부터 시작하여 dist 배열에다가 1씩 추가하면 된다.
- 그러고 dist 배열 값 중에 K와 일치하는 값이 있다면 출력
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Main {
static int dist[];
static ArrayList<ArrayList<Node>> graph = new ArrayList<>();
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
StringBuilder sb = new StringBuilder();
boolean result = false;
int N = Integer.parseInt(st.nextToken()); //도시의 개수
int M = Integer.parseInt(st.nextToken()); //도록의 개수
int K = Integer.parseInt(st.nextToken()); // 거리 정보
int X = Integer.parseInt(st.nextToken()); //시작
for (int i = 0; i <= N ; i++) {
graph.add(new ArrayList<>());
}
for (int i = 0; i < M ; i++) {
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
graph.get(start).add(new Node(end,1));
}
dist = new int[N+1];
Arrays.fill(dist,Integer.MAX_VALUE);
solution(X);
for (int i = 0; i <= N; i++) {
if(dist[i] != Integer.MAX_VALUE && dist[i] == K){
sb.append(i).append("\n");
result = true;
}
}
if(result){
System.out.println(sb);
}else{
System.out.println("-1");
}
}
private static void solution(int k) {
PriorityQueue<Node> queue = new PriorityQueue<>(((o1, o2) -> o1.cost - o2.cost));
queue.add(new Node(k,0));
dist[k] = 0;
while (!queue.isEmpty()){
Node now = queue.poll();
for(Node next : graph.get(now.v)){
if(dist[next.v] > dist[now.v] + next.cost){
dist[next.v] = dist[now.v] + next.cost;
queue.add(new Node(next.v, dist[next.v]));
}
}
}
}
static class Node{
int v;
int cost;
public Node(int v,int cost){
this.v = v;
this.cost= cost;
}
}
}'알고리즘' 카테고리의 다른 글
| 백준 No.1446 지름길 - JAVA (0) | 2023.03.01 |
|---|---|
| 백준 No.6550 부분 문자열 - JAVA (0) | 2023.02.28 |
| 백준 No.1417 국회의원 선거 - JAVA (0) | 2023.02.27 |
| 백준 No.1012 유기농 배추 - JAVA (0) | 2023.02.27 |
| 백준 No.1261 알고스팟 - JAVA (0) | 2023.02.27 |